Representation in Python

The basic guiding principle for us in translating state space models into Python is to allow users to focus on the specification aspect of their model rather than on the machinery of efficient and accurate filtering and smoothing computation. To do this, we apply the programmatic technique of object oriented programming (OOP). While a full description and motivation of OOP is beyond the scope of this paper, one of the primary benefits for our purposes is that it facilitates organization and prevents the writing and rewriting of the same or similar code. This feature is quite attractive in general, but as will be shown below, state space models fit particularly well into - and reap substantial benefits from - the object oriented paradigm. For state space models, filtering, smoothing, a large part of parameter estimation, and some postestimation results are standard; they depend only on the generic form of the model given in (?) rather than the specializations found in, for example, (?), (?), and (?)).

The Python programming language is general-purpose, interpreted, dynamically typed, and high-level. Relative to other programming languages commonly used for statistical computation, it has both strengths and weaknesses. It lacks the breadth of available statistical routines present in the R programming language, but instead features a core stack of well-developed scientific libraries. Since it began life as a general purpose programming language, it lacks the native understanding of matrix algebra which makes MATLAB so easy to begin working with (these features are available, but are provided by the the Numeric Python (NumPy) and Scientific Python (SciPy) libraries) but it has more built-in features for working with text, files, web sites, and more. All of Python, R, and MATLAB feature excellent graphing and plotting features and the ability to integrate compiled code for faster performance.

Of course, anything that can be done in one language can in principle be done in many others, so familiarity, style, and tradition play a substantial role in determining which language is used in which discipline. There is much to recommend R, MATLAB, Stata, Julia, and other languages. Nonetheless, it is hoped that this paper will not only show how state space models can be specified and estimated in Python, but also introduce some of the powerful and elegent features of Python that make it a strong candidate for consideration in a wide variety of statistical computing projects.

Object oriented programming

What follows is a brief description of the concepts of object oriented programming. The content follows [33], which may be consulted for more detail. The Python Language Reference may be consulted for details on the implementation and syntax of object oriented programming specific to Python.

Objects are “collections of operations that share a state” ([33]). Another way to put it is that objects are collections of data (the “state”) along with functions that manipulate or otherwise make use of that data (the “operations”). In Python, the data held by an object are called its attributes and the operations are called its methods. An example of an object is a point in the Cartesian plane, where we define the “state” of the point as its coordinates in the plane and define two methods, one to change its \(x\)-coordinate to \(x + dx\), and one to change the \(y\)-coordinate to \(y + dy\).

Classes are “templates from which objects can be created ... whereas the [attributes of an] object represent actual variables, class [attributes] are potential, being instantiated only when an object is created” (Ibid.). The point object described above could be written in Python code as follows. First, a Point class is defined, providing the template for all actual points that will later be represented.

# This is the class definition. Object oriented programming has the concept
# of inheritance, whereby classes may be "children" of other classes. The
# parent class is specified in the parentheses. When defining a class with
# no parent, the base class `object` is specified instead.
class Point(object):

    # The __init__ function is a special method that is run whenever an
    # object is created. In this case, the initial coordinates are set to
    # the origin. `self` is a variable which refers to the object instance
    # itself.
    def __init__(self):
        self.x = 0
        self.y = 0

    def change_x(self, dx):
        self.x = self.x + dx

    def change_y(self, dy):
        self.y = self.y + dy

With the template defined, we can create as many Point objects (instantiations of the Point template), with actual data, as we like. Below, point_object holds an actual instance of a point with coordinates first at \((0, 0)\) and then at \((-2, 0)\).

# An object of class Point is created
point_object = Point()

# The object exposes it's attributes
print(point_object.x)  # 0

# And we can call the object's methods
# Notice that although `self` is the first argument of the class method,
# it is automatically populated, and we need only specify the other
# argument, `dx`.
point_object.change_x(-2)
print(point_object.x)  # -2

Object oriented programming allows code to be organized hierarchically through the concept of class inheritance, whereby a class can be defined as an extension to an existing class. The existing class is called the parent and the new class is called the child. [33] writes “inheritance allows us to reuse the behavior of a class in the definition of new classes. Subclasses of a class inherit the operations of their parent class and may add new operations and new [attributes]”.

Through the mechanism of inheritance, a parent class can be defined with a set of generic functionality, and then many child classes can subsequently be defined with specializations. Each child thus contains both the generic functionality of the parent class as well as its own specific functionality. Of course the child classes may have children of their own, and so on.

As an example, consider creating a new class describing vectors in \(\mathbb{R}^2\). Since a vector can be described as an ordered pair of coordinates, the Point class defined above could also be used to describe vectors and allow users to modify the vector using the change_x and change_y methods. Suppose that we wanted to add a method to calculate the length of the vector. It would not make sense to add a length method to the Point class, since a point does not have a length, but we can create a new Vector class extending the Point class with the new method. In the code below, we also introduce arguments into the class constructor (the __init__ method).

# This is the new class definition. Here, the parent class, `Point`, is in
# the parentheses.
class Vector(Point):

    def __init__(self, x, y):
        # Call the `Point.__init__` method to initialize the coordinates
        # to the origin
        super(Vector, self).__init__()

        # Now change to coordinates to those provided as arguments, using
        # the methods defined in the parent class.
        self.change_x(x)
        self.change_y(y)

    def length(self):
        # Notice that in Python the exponentiation operator is a double
        # asterisk, "**"
        return (self.x**2 + self.y**2)**0.5

# An object of class Vector is created
vector_object = Vector(1, 1)
print(vector_object.length())  # 1.41421356237

Returning to state space models and Kalman filtering and smoothing, the object oriented approach allows for separation of concerns and prevents duplication of effort. The base classes contain the functionality common to all state space models, in particular Kalman filtering and smoothing routines, and child classes fill in model-specific parameters into the state space representation matrices. In this way, users need only specify the parts that are absolutely necessary and yet the classes they define contain full state space operations. In fact, many additional features beyond filtering and smoothing are available through the base classes, including methods for estimation of unknown parameters, summary tables, prediction and forecasting, model diagnostics, simulation, and impulse response functions.

Representation

In this section we present a prototypical example in which we create a subclass specifying a particular model. That subclass then inherits state space functionality from its parent class. Tables detailing the attributes and methods that are available through inheritance of the parent class are provided in Appendix B: Inherited attributes and methods.

The parent class is sm.tsa.statespace.MLEModel (referred to as simply MLEModel in what follows), and it provides an interface to the state space functionality described above. Subclasses are required to specify the state space matrices of the model they implement (i.e. the elements from Table 1) and in return they receive a number of built-in functions that can be called by users. The most important of these are update, loglike, filter, smooth, and simulation_smoother.

The first, update, accepts as arguments parameters of the model (for example the \(\phi\) autoregressive parameter of the ARMA(1, 1) model) and updates the underlying state space system matrices with those parameters. Note that the second, third, and fourth methods, described just below, implicitly call update as part of their operation.

The second, loglike, performs the Kalman filter recursions and returns the joint loglikelihood of the sample. The third, filter, performs the Kalman filter recursions and returns an object holding the full output of the filter (see Table 2), as well as the state space representation (see Table 1). The fourth, smooth, performs Kalman filtering and smoothing recursions and returns an object holding the full output of the smoother (see Table 3) as well as the filtering output and the state space representation. The last, simulation_smoother, creates a new object that can be used to create an arbitrary number of simulated state and disturbance series (see Table 4).

The first four methods - update, loglike, filter, and smooth - require as their first argument a parameter vector at which to perform the operation. They all first update the state space system matrices, and then the latter three perform the appropriate additional operation. The simulation_smoother method does not require the parameter vector as an argument, since it performs simulations based on whatever parameter values have been most recently set, either by one of the other three methods or by the update method.

As an example of the use of this class, consider the following code, which constructs a local level model for the Nile data with known parameter values (the next section will consider parameter estimation) and then applies the above methods. Recall that to fully specify a state space model, all of the elements from Table 1 must be set and the Kalman filter must be initialized. For subclasses of MLEModel, all state space elements are created as zero matrices of the appropriate shapes; often only the non-zero elements need be specified. [1]

# Create a new class with parent sm.tsa.statespace.MLEModel
class LocalLevel(sm.tsa.statespace.MLEModel):

    # Define the initial parameter vector; see update() below for a note
    # on the required order of parameter values in the vector
    start_params = [1.0, 1.0]

    # Recall that the constructor (the __init__ method) is
    # always evaluated at the point of object instantiation
    # Here we require a single instantiation argument, the
    # observed dataset, called `endog` here.
    def __init__(self, endog):
        super(LocalLevel, self).__init__(endog, k_states=1)

        # Specify the fixed elements of the state space matrices
        self['design', 0, 0] = 1.0
        self['transition', 0, 0] = 1.0
        self['selection', 0, 0] = 1.0

        # Initialize as approximate diffuse, and "burn" the first
        # loglikelihood value
        self.initialize_approximate_diffuse()
        self.loglikelihood_burn = 1

    # Here we define how to update the state space matrices with the
    # parameters. Note that we must include the **kwargs argument
    def update(self, params, **kwargs):
        # Using the parameters in a specific order in the update method
        # implicitly defines the required order of parameters
        self['obs_cov', 0, 0] = params[0]
        self['state_cov', 0, 0] = params[1]

# Instantiate a new object
nile_model_1 = LocalLevel(nile)

Three elements of the above code merit discussion. First, we have included a class attribute start_params, which will later be used by the model when performing maximum likelihood estimation. [2] Second, note that the signature of the update method includes **kwargs as an argument. This allows it to accept an arbitrary set of keyword arguments, and this is required to allow handling of parameter transformations (discussed below). It is important to remember that in all subclasses of MLEModel, the update method signature must include **kwargs.

Second, the state space representation matrices are set using so-called “slice notation”, such as self['design'], rather than the so-called “dot notation” that is usually used for attribute and method access, such as self.loglikelihood_burn. Although it is possible to access and set state space matrices and their elements using dot notation, slice notation is strongly recommended for technical reasons. [3] Note that only the state space matrices can be set using slice notation (see Table 9 for the list of attributes that can be set with slice notation).

This class LocalLevel fully specifies the local level state space model. At our disposal now are the methods provided by the parent MLEModel class. They can be applied as follows.

First, the loglike method returns a single number, and can be evaluated at various sets of parameters.

# Compute the loglikelihood at values specific to the nile model
print(nile_model_1.loglike([15099.0, 1469.1]))  # -632.537695048

# Try computing the loglikelihood with a different set of values; notice that it is different
print(nile_model_1.loglike([10000.0, 1.0]))  # -687.5456216

The filter method returns an object from which filter output can be retrieved.

# Retrieve filtering output
nile_filtered_1 = nile_model_1.filter([15099.0, 1469.1])
# print the filtered estimate of the unobserved level
print(nile_filtered_1.filtered_state[0])         # [ 1103.34065938  ... 798.37029261 ]
print(nile_filtered_1.filtered_state_cov[0, 0])  # [ 14874.41126432  ... 4032.15794181 ]

The smooth method returns an object from which smoother output can be retrieved.

# Retrieve smoothing output
nile_smoothed_1 = nile_model_1.smooth([15099.0, 1469.1])
# print the smoothed estimate of the unobserved level
print(nile_smoothed_1.smoothed_state[0])         # [ 1107.20389814 ... 798.37029261 ]
print(nile_smoothed_1.smoothed_state_cov[0, 0])  # [ 4015.96493689  ... 4032.15794181 ]

Finally the simulation_smoother method returns an object that can be used to simulate state or disturbance vectors via the simulate method.

# Retrieve a simulation smoothing object
nile_simsmoother_1 = nile_model_1.simulation_smoother()

# Perform first set of simulation smoothing recursions
nile_simsmoother_1.simulate()
print(nile_simsmoother_1.simulated_state[0, :-1])  # [ 1000.09720165 ... 882.30604412 ]

# Perform second set of simulation smoothing recursions
nile_simsmoother_1.simulate()
print(nile_simsmoother_1.simulated_state[0, :-1])  # [ 1153.62271051 ... 808.43895425 ]

Fig. 4 plots the observed data, filtered series, smoothed series, and the simulated level from ten simulations, generated from the above model.

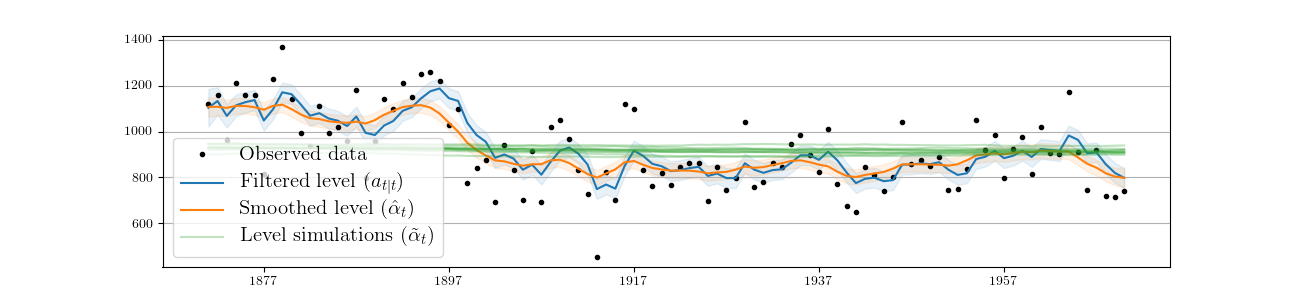
Fig. 4 Filtered and smoothed estimates and simulatations of unobserved level for Nile data.

[1]	More specifically, potentially time-varying matrices are created as zero matrices of the appropriate non-time-varying shape. If a time-varying matrix is required, the whole matrix must be re-created in the appropriate time-varying shape before individual elements may be modified.

[2]

It may seem restrictive to require the initial parameter value to be a a class attribute, which is set to a specific value. In practice, the attribute can be replaced with a class property, allowing dynamic creation of the attribute’s value. In this way the initial parameter vector for an ARMA(p,q) model could, for example, be generated using ordinary least squares.

[3]

The difference between self['design', 0, 0] = 1 and self.design[0,0] = 1 lies in the order of operations. With dot notation (the latter example) first the self.design matrix is accessed and then the [0,0] element of that matrix is accessed. With slice notation, a class method (__setitem__) is given the matrix name and the [0,0] element simultaneously. Usually there is no difference between the two approaches, but, for example, if the matrix in question has a floating point datatype and the new value is a complex number, then only the real component of that new value will be set in the matrix and a warning will be issued. This problem does not occur with the slice notation.

Additional remarks

Once a subclass has been created, it has access to a variety of features from the base (parent) classes. A few remarks about available features are merited.

First, if the model is time-invariant, then a check for convergence will be used at each step of the Kalman filter iterations. Once convergence has been achieved, the converged state disturbance covariance matrix, Kalman gain, and forecast error covariance matrix are used at all remaining iterations, reducing the computational burden. The tolerance for determining convergence is controlled by the tolerance attribute, which is initially set to \(10^{-19}\) but can be changed by the user. For example, to disable the use of converged values in the model above one could use the code nile_model_3.tolerance = 0.

Second, two recent innovations in Kalman filtering are available to handle large-dimensional observations. These include the univariate filtering approach of [19] and the collapsed approach of [14]. The use of these approaches are controlled by the set_filter_method method. For example, to enable both of these approaches in the Nile model, one could use the code nile_model_3.set_filter_method(filter_univariate=True, filter_collapsed=True) (this is just for illustration, since of course there is only a single variable in that model so that these options would have no practical effect).

Next, options to enable conservation of computer memory (RAM) are available and are controllable via the set_conserve_memory method. It should be noted that the usefulness of these options depends on the analysis required by the user because smoothing requires all filtering values and simulation smoothing requires all smoothing and filtering values. However, in maximum likelihood estimation or Metropolis-Hastings posterior simulation, all that is required is the joint likelihood value. One might enable memory conservation until optimal parameters have been found and then disable it so as to calculate any filtered and smoothed values of interest. In Gibbs sampling MCMC approaches, memory conservation is not available because the simulation smoother is required.

Fourth, predictions and impulse response functions are immediately available for any state space model through the filter results object (obtained as the returned value from a filter call), through the predict and impulse_responses methods. These will be demonstrated below.

Fifth, the Kalman filter (and smoothers) are fully equipped to handle missing observation data; no special code is required.

Finally, before moving on to specific parameter estimation methods it is important to note that the simulation smoother object created via the simulation_smoother method generates simulations based on the state space matrices as they are defined when the simulation is performed and not when the simulate method was called. This will be important when implementing Gibbs sampling MCMC parameter estimation methods. As an illustration, consider the following code:

# BEFORE: Perform some simulations with the original parameters
nile_simsmoother_1 = nile_model_1.simulation_smoother()
nile_model_1.update([15099.0, 1469.1])
nile_simsmoother_1.simulate()
# ...

# AFTER: Perform some new simulations with new parameters
nile_model_1.update([10000.0, 1.0])
nile_simsmoother_1.simulate()
# ...

Fig. 5 plots ten simulations generated during the BEFORE period, and ten simulations from the AFTER period. It is clear that they are simulating different series, reflecting the different parameters values in place at the time of simulation.

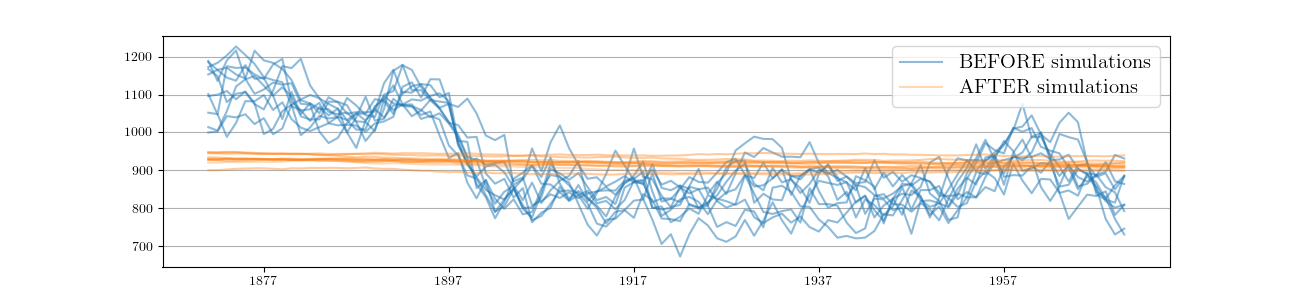
Fig. 5 Simulations of the unobserved level for Nile data under two different parameter sets.

Practical considerations

As described before, two practical considerations with the Kalman filter are numerical stability and performance. Briefly discussed were the availability of a square-root filter and the use of compiled computer code. In practice, the square-root filter is rarely required, and this Python implementation does not use it. One good reason for this is that “the amount of computation required is substantially larger” ([10]), and acceptable numerical stability for most models is usually achieved via enforced symmetry of the state covariance matrix (see [11], for example).

High performance is achieved primarily through the use of Cython ([3]). Cython allows suitably modified Python code to be compiled to C, in some cases (such as the current one) dramatically improving performance. Note that compiled code for performance-critical computation is also available in several of the other Kalman filtering implementations mentioned in the introduction. Other performance-related features, such as the recent advances in filtering with large-dimensional observations described in the preceding section, are also available.

An additional practical consideration whenever computer code is at issue is the possibility of programming errors (“bugs”). [22] emphasize the need for tests ensuring accurate results, as well as good documentation and the availability of source code so that checking for bugs is possible. The source code for this implementation is available, with reasonably extensive inline comments describing procedures. Furthermore, even though the spectre of bugs cannot be fully exorcised, over a thousand “unit tests” have been written, and are available for users to run themselves, comparing output to known results from a variety of outside sources. These tests are run continuously with the software’s development to prevent errors from creeping in.

At this point, we once again draw attention to the separation of concerns made possible by the implementation approach pursued here. Although writing the code for a conventional Kalman filter is relatively trivial, writing the code for a Kalman filter, smoother, and simulation smoother using the univariate and collapsed approaches, properly allowing for missing data, and in a compiled language to achieve acceptable performance is not. And yet, for models in state space form, the solution, once created, is entirely generic. The use of an object oriented approach here is what allows users to have the best of both worlds: classes can be custom designed using only Python and yet they contain methods (loglike, filter, etc.) which have been written and compiled for high performance and tested for accuracy.

Example models

In this section, we provide code describing the example models in the previous sections. This code is provided to illustrate the above principles in specific models, and it is not necessarily the best way to develop these models. For example, it is more efficient to develop a single class to handle all ARMA(p,q) models at once rather than separate classes for different orders. [4]

[4]	See the SARIMAX class described in Out-of-the-box models for a fully featured class built-in to Statsmodels that allows estimating a large set of models, including ARMA(p, q).

ARMA(1, 1) model

The following code is a straightforward translation of (?). Notice that here the state dimension is 2 but the dimension of the state disturbance is only 1; this is represented in the code by setting k_states=2 but k_posdef=1. [5] Also demonstrated is the possibility of specifying the Kalman filter initialization in the class construction call with the argument initialization='stationary'. [6]

class ARMA11(sm.tsa.statespace.MLEModel):

    start_params = [0, 0, 1]

    def __init__(self, endog):
        super(ARMA11, self).__init__(
            endog, k_states=2, k_posdef=1, initialization='stationary')

        self['design', 0, 0] = 1.
        self['transition', 1, 0] = 1.
        self['selection', 0, 0] = 1.

    def update(self, params, **kwargs):
        self['design', 0, 1] = params[1]
        self['transition', 0, 0] = params[0]
        self['state_cov', 0, 0] = params[2]

# Example of instantiating a new object, updating the parameters to the
# starting parameters, and evaluating the loglikelihood
inf_model = ARMA11(inf)
print(inf_model.loglike(inf_model.start_params))  # -2682.72563702

Local level model

The class for the local level model was defined in the previous section.

Real business cycle model

The real business cycle model is specified by the equations (?). It again has a state dimension of 2 and a state disturbance dimension of 1, and again the process is assumed to be stationary. Unlike the previous examples, here the (structural) parameters of the model do not map directly to elements of the system matrices. As described in the definition of the RBC model, the thirteen reduced form parameters found in the state space matrices are non-linear functions of the six structural parameters. We want to set up the model in terms of the structural parameters and use the update method to perform the appropriate transformations to retrieve the reduced form parameters. This is important because the theory does not allow the reduced form parameters to vary arbitrarily; in particular, only certain combinations of the reduced form parameters are consistent with generation from the underlying structural parameters through the model.

Solving the structural model for the reduced form parameters in terms of the structural parameters requires the solution of a linear rational expectations model, and a full description of this process is beyond the scope of this paper. This particular RBC model can be solved using the method of [4]; more general solution methods exist for more general models (see for example [17] and [29]).

Regardless of the method used, for many linear (or linearized) models the solution will be in state space form and so the state space matrices can be updated with the reduced form parameters. For expositional purposes, the following code snippet is not complete, but shows the general formulation in Python. A complete version of the class is found in Appendix C: Real business cycle model code.

class SimpleRBC(sm.tsa.statespace.MLEModel):

    start_params = [...]

    def __init__(self, endog):
        super(SimpleRBC, self).__init__(
            endog, k_states=2, k_posdef=1, initialization='stationary')

        # Initialize RBC-specific variables, parameters, etc.
        # ...

        # Setup fixed elements of the statespace matrices
        self['selection', 1, 0] = 1

    def solve(self, structural_params):
        # Solve the RBC model
        # ...

    def update(self, params, **kwargs):
        params = super(SimpleRBC, self).update(params, **kwargs)

        # Reconstruct the full parameter vector from the
        # estimated and calibrated parameters
        structural_params = ...
        measurement_variances = ...

        # Solve the model
        design, transition = self.solve(structural_params)

        # Update the statespace representation
        self['design'] = design
        self['obs_cov', 0, 0] = measurement_variances[0]
        self['obs_cov', 1, 1] = measurement_variances[1]
        self['obs_cov', 2, 2] = measurement_variances[2]
        self['transition'] = transition
        self['state_cov', 0, 0] = structural_params[...]

[5]

The dimension of the state disturbance is named k_posdef because the selected state disturbance vector is given not by \(\eta_t\) but by \(R_t \eta_t\). The dimension of the selected state disturbance vector is always equal to the dimension of the state, but the selected state disturbance covariance matrix will be have k_states - k_posdef zero-eigenvalues. Thus the dimension of the state disturbance gives the dimension of the subset of the selected state disturbance for which a positive definite covariance matrix; hence the name k_posdef.

[6]

Of course the assumption of stationarity would be violated for certain parameter values, for example if \(\phi = 1\). This has important implications for parameter estimation where we typically want to only allow parameters inducing a stationary model. This is discussed in the specific sections on parameter estimation.