State space models¶
The state space representation of a possibly time-varying linear and Gaussian time series model can be written as
where \(y_t\) is observed, so the first equation is called the observation or measurement equation, and \(\alpha_t\) is unobserved. The second equation describes the transition of the unobserved state, and so is called the transition equation. The dimensions of each of the objects, as well as the name by which we will refer to them, are given in Table 1. All notation in this paper will follow that in [7] and [10].
| Object | Description | Dimensions |
|---|---|---|
| \(y_t\) | Observed data | \(p \times 1\) |
| \(\alpha_t\) | Unobserved state | \(m \times 1\) |
| \(d_t\) | Observation intercept | \(p \times 1\) |
| \(Z_t\) | Design matrix | \(p \times m\) |
| \(\varepsilon_t\) | Observation disturbance | \(p \times 1\) |
| \(H_t\) | Observation disturbance covariance matrix | \(p \times p\) |
| \(c_t\) | State intercept | \(m \times 1\) |
| \(T_t\) | Transition matrix | \(m \times m\) |
| \(R_t\) | Selection matrix | \(m \times r\) |
| \(\eta_t\) | State disturbance | \(r \times 1\) |
| \(Q_t\) | State disturbance covariance matrix | \(r \times r\) |
The model is called time-invariant if only \(y_t\) and \(\alpha_t\) depend on time (so, for example, in a time-invariant model \(Z_t = Z_{t+1} \equiv Z\)). In the case of a time-invariant model, we will drop the time subscripts from all state space representation matrices. Many important time series models are time-invariant, including ARIMA, VAR, unobserved components, and dynamic factor models.
Kalman Filter¶
The Kalman filter, as applied to the state space model above, is a recursive formula running forwards through time (\(t = 1, 2, \dots, n\)) providing optimal estimates of the unknown state. [1] At time \(t\), the predicted quantities are the optimal estimates conditional on observations up to \(t-1\), and the filtered quantities are the optimal estimates conditional on observations up to time \(t\). This will be contrasted below with smoothed quantities, which are optimal estimates conditional on the full sample of observations.
We now define some notation that will be useful below. Define the vector of all observations up to time \(s\) as \(Y_s = \{ y_1, \dots, y_s \}\). Then the distribution of the predicted state is \(\alpha_t \mid Y_{t-1} \sim N(a_t, P_t)\), and the distribution of the filtered state is \(\alpha_t \mid Y_{t} \sim N(a_{t|t}, P_{t|t})\).
As shown in, for example, [10], the Kalman filter applied to the model (1) above yields a recursive formulation. Given prior estimates \(a_t, P_t\), the filter produces optimal filtered and predicted estimates (\(a_{t|t}, P_{t|t}\) and \(a_{t+1}, P_{t+1}\), respectively) as follows
An important byproduct of the Kalman filter iterations is evaluation of the loglikelihood of the observed data due to the so-called “prediction error decomposition”.
The dimensions of each of the objects, as well as the name by which we will refer to them, are given in Table 2. Also included in the table is the Kalman gain, which is defined as \(K_t = T_t P_t Z_t' F_t^{-1}\).
| Object | Description | Dimensions |
|---|---|---|
| \(a_t\) | Prior state mean | \(m \times 1\) |
| \(P_t\) | Prior state covariance | \(m \times m\) |
| \(v_t\) | Forecast error | \(p \times 1\) |
| \(F_t\) | Forecast error covariance matrix | \(p \times p\) |
| \(a_{t|t}\) | Filtered state mean | \(m \times 1\) |
| \(P_{t|t}\) | Filtered state covariance matrix | \(m \times m\) |
| \(a_{t+1}\) | Predicted state mean | \(m \times 1\) |
| \(P_{t+1}\) | Predicted state covariance matrix | \(m \times m\) |
| \(\log L(Y_n)\) | Loglikelihood | scalar |
| \(K_t\) | Kalman gain | \(m \times p\) |
| [1] | In this paper, “optimal” can be interpreted in the sense of minimizing the mean-squared error of estimation. In chapter 4, [10] show three other senses in which optimal can be defined for this same model. |
Initialization¶
Notice that since the Kalman filter is a recursion, for \(t = 2, \dots, n\) the prior state mean and prior state covariance matrix are given as the output of the previous recursion. For \(t = 1\), however, no previous recursion has been yet applied, and so the mean \(a_1\) and covariance \(P_1\) of the distribution of the initial state \(\alpha_1 \sim N(a_1, P_1)\) must be specified. The specification of the distribution of the initial state is referred to as initialization.
There are four methods typically used to initialize the Kalman filter: (1) if the distribution is known or is otherwise specified, initialize with the known values; (2) initialize with the unconditional distribution of the process (this is only applicable to the case of stationary state processes); (3) initialize with a diffuse (i.e. infinite variance) distribution; (4) initialize with an approximate diffuse distribution, i.e. \(a_1 = 0\) and \(P_1 = \kappa I\) where \(\kappa\) is some large constant (for example \(\kappa = 10^6\)). When the state has multiple elements, a mixture of these four approaches can be used, as appropriate.
Of course, if options (1) or (2) are available, they are preferred. In the case that there are non-stationary components with unknown initial distribution, either (3) or (4) must be employed. While (4) is simple to use, [10] note that “while the device can be useful for approximate exploratory work, it is not recommended for general use since it can lead to large rounding errors;” for that reason they recommend using exact diffuse initialiation. For more about initialization, see [20] and chapter 5 of [10].
Note that when diffuse initialization is applied, a number of initial loglikelihood values are excluded (“burned”) when calculating the joint loglikelihood, as they are considered under the influence of the diffuse states. In exact diffuse initialization the number of burned periods is determined in initialization, but in the approximate case it must be specified. In this case, it is typically set equal to the dimension of the state vector; it turns out that this often coincides with the value in the exact case.
State and disturbance smoothers¶
The state and disturbance smoothers, as applied to the state space model above, are recursive formulas running backwards through time (\(t = n, n-1, \dots, 1\)) providing optimal estimates of the unknown state and disturbance vectors based on the full sample of observations.
As developed in [21] and Chapter 4 of [10], following an application of the Kalman filter (yielding the predicted and filtered estimates of the state) the smoothing recursions can be written as (where \(L_t = T_t - K_t Z_t\))
The dimensions of each of the objects, as well as the name by which we will refer to them, are given in Table 3.
| Object | Description | Dimensions |
|---|---|---|
| \(\hat \alpha_t\) | Smoothed state mean | \(m \times 1\) |
| \(V_t\) | Smoothed state covariance matrix | \(m \times m\) |
| \(\hat \varepsilon_t\) | Smoothed observation disturbance mean | \(p \times 1\) |
| \(Var(\varepsilon_t \mid Y_n)\) | Smoothed observation disturbance covariance matrix | \(p \times p\) |
| \(\hat \eta_t\) | Smoothed state disturbance mean | \(m \times 1\) |
| \(Var(\eta_t \mid Y_n)\) | Smoothed state disturbance covariance matrix | \(m \times m\) |
| \(u_t\) | Smoothing error | \(p \times 1\) |
| \(r_{t-1}\) | Scaled smoothed estimator | \(m \times 1\) |
| \(N_{t-1}\) | Scaled smoothed estimator covariance matrix | \(m \times m\) |
Simulation smoother¶
The simulation smoother, developed in [9] and Chapter 4 of [10], allows drawing samples from the distributions of the full state and disturbance vectors, conditional on the full sample of observations. It is an example of a “forwards filtering, backwards sampling” algorithm because one application of the simulation smoother requires one application each of the Kalman filter and state / disturbance smoother. An often-used alternative forwards filtering, backwards sampling algorithm is that of [5].
The output of the simulation smoother is the drawn samples; the dimensions of each of the objects, as well as the name by which we will refer to them, are given in Table 4.
| Object | Description | Dimensions |
|---|---|---|
| \(\tilde \alpha_t\) | Simulated state | \(m \times 1\) |
| \(\tilde \varepsilon_t\) | Simulated observation disturbance | \(p \times 1\) |
| \(\tilde \eta_t\) | Simulated state disturbance | \(m \times 1\) |
Practical considerations¶
There are a number of important practical considerations associated with the implementation of the Kalman filter and smoothers in computer code. Two of the most important are numerical stability and computational speed; these issues are briefly described below, but will be revisited when the Python implementation is discussed.
In the context of the Kalman filter, numerical stability usually refers to the possibility that the recursive calculations will not maintain the positive definiteness or symmetry of the various covariance matrices. Numerically stable routines can be used to mitigate these concerns, for example using linear solvers rather than matrix inversion. In extreme cases a numerically stable Kalman filter, the so-called square-root Kalman filter, can be used (see [25] or chapter 6.3 of [10]).
Performance can be an issue because the Kalman filter largely consists of iterations (loops) and matrix operations, and it is well known that loops perform poorly in interpreted languages like MATLAB and Python. [2] Furthermore, regardless of the high-level programming language used, matrix operations are usually ultimately performed by the highly optimized BLAS and LAPACK libraries written in Fortran. For performant code, compiled languages are preferred, and code should directly call the BLAS and LAPACK libraries directly when possible, rather than through intermediate functions (for details on the BLAS and LAPACK libraries, see [1]).
| [2] | The availability of a just-in-time (JIT) compiler can help with loop performance in interpreted languages; one is integrated into MATLAB, and the Numba project introduces one into Python. |
Additional remarks¶
Several additional remarks are merited about the Kalman filter. First, under certain conditions, for example a time-invariant model, the Kalman filter will converge, meaning that the predicted state covariance matrix, the forecast error covariance matrix, and the Kalman gain matrix will all reach steady-state values after some number of iterations. This can be exploited to improve performance.
The second remark has to do with missing data. In the case of completely or partially missing observations, not only can the Kalman filter proceed with making optimal estimates of the state vector, it can provide optimal estimates of the missing data.
Third, the state space approach can be used to obtain optimal forecasts and to explore impulse response functions.
Finally, the state space approach can be used for parameter estimation, either through classical methods (for example maximum likelihood estimation) or Bayesian methods (for example posterior simulation via Markov chain Monte Carlo). This will be described in detail in sections 4 and 5, below.
Example models¶
As mentioned above, many important time series models can be represented in state space form. We present three models in detail to use as examples: an autoregressive moving average (ARMA) model, the local level model, and a simple real business cycle (RBC) dynamic stochastic general equilibrium (DSGE) model.
In fact, general versions of several time series models have already been implemented in Statsmodels and are available for use (see Out-of-the-box models for details). However, since the goal here is to provide information sufficient for users to specify and estimate their own custom models, we emphasize the translation of a model from state space formulation to Python code. Below we present state space representations mathematically, and in subsequent sections we describe their representation in Python code.
ARMA(1, 1) model¶
Autoregressive moving average models are widespread in the time series literature, so we will assume the reader is familiar with their basic motivation and theory. Suffice it to say, these models are often successfully applied to obtain reduced form estimates of the dynamics exhibited by time series and to produce forecasts. For more details, see any introductory time series text.
An ARMA(1,1) process (where we suppose \(y_t\) has already been demeaned) can be written as
It is well known that any autoregressive moving average model can be represented in state-space form, and furthermore that there are many equivalent representations. Below we present one possible representation based on [12], with the corresponding notation from (1) given below each matrix.
One feature of ARMA(p,q) models generally is that if the assumption of stationarity holds, the Kalman filter can be initialized with the unconditional distribution of the time series.
As an application of this model, in what follows we will consider applying an ARMA(1,1) model to inflation (first difference of the logged US consumer price index). This data can be obtained from the Federal Reserve Economic Database (FRED) produced by the Federal Reserve Bank of St. Louis. In particular, this data can be easily obtained using the Python package pandas-datareader. [3]
from pandas_datareader.data import DataReader
cpi = DataReader('CPIAUCNS', 'fred', start='1971-01', end='2016-12')
cpi.index = pd.DatetimeIndex(cpi.index, freq='MS')
inf = np.log(cpi).resample('QS').mean().diff()[1:] * 400
Fig. 1 shows the resulting time series.
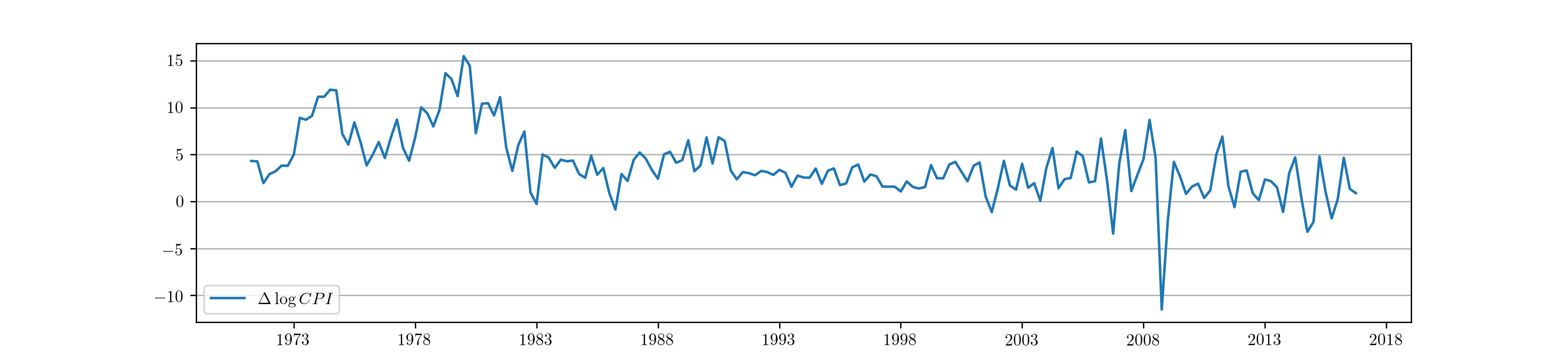
Fig. 1 Time path of US CPI inflation from 1971:Q1 - 2016:Q4.
| [3] | This is for illustration purposes only, since an ARMA(1, 1) model with mean zero is not a good model for quarterly CPI inflation. |
Local level model¶
The local level model generalizes the concept of intercept (i.e. “level”) in a linear regression to be time-varying. Much has been written about this model, and the second chapter of [10] is devoted to it. It can be written as
This is already in state space form, with \(Z = T = R = 1\). This model is not stationary (the unobserved level follows a random walk), and so stationary initialization of the Kalman filter is impossible. Diffuse initialization, either approximate or exact, is required.
As an application of this model, in what follows we will consider applying the local level model to the annual flow volume of the Nile river between 1871 and 1970. This data is freely available from many sources, and is included in many econometrics analysis packages. Here, we use the data from the Python package Statsmodels.
nile = sm.datasets.nile.load_pandas().data['volume']
nile.index = pd.date_range('1871', '1970', freq='AS')
Fig. 2 shows the resulting time series.
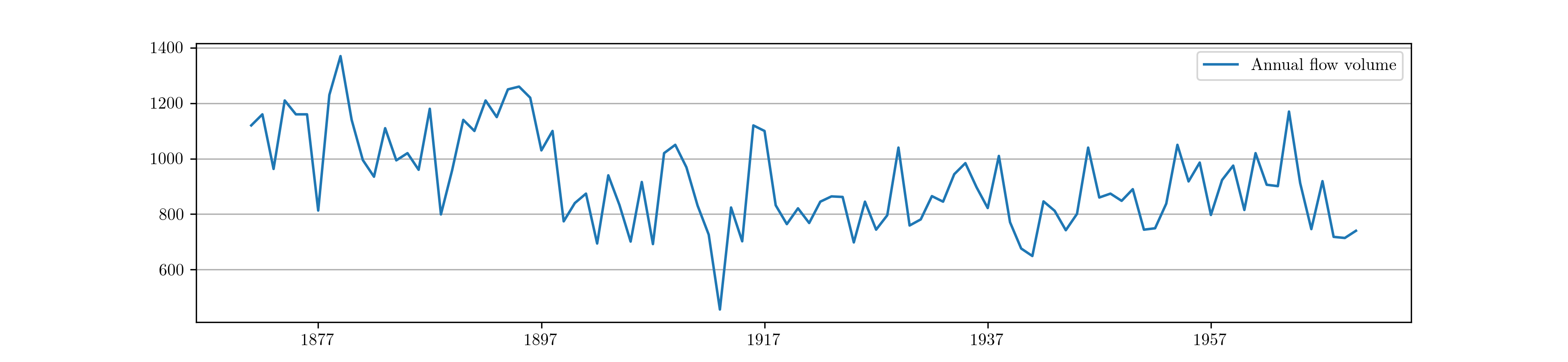
Fig. 2 Annual flow volume of the Nile river 1871 - 1970.
Real business cycle model¶
Linearized models can often be placed into state space form and evaluated using the Kalman filter. A very simple real business cycle model can be represented as [4]
where \(y_t\) is output, \(n_t\) is hours worked, \(c_t\) is consumption, \(k_t\) is capital, and \(z_t\) is a technology shock process. In this formulation, output, hours worked, and consumption are observable whereas the capital stock and technology process are unobserved. This model can be developed as the linearized output of a fully microfounded DSGE model, see for example [27] or [8]. In the theoretical model, the variables are assumed to be stationary.
There are six structural parameters of this RBC model: the discount rate, the marginal disutility of labor, the depreciation rate, the capital-share of output, the technology shock persistence, and the technology shock innovation variance. It is important to note that the reduced form parameters of the state space representation (for example \(\phi_{yk}\)) are complicated and non-linear functions of these underlying structural parameters.
The raw observable data can be obtained from FRED, although it must be transformed to be consistent with the model (for example to induce stationarity). For an explanation of the datasets used and the transformations, see either of the two references above.
from pandas_datareader.data import DataReader
start = '1984-01'
end = '2016-09'
labor = DataReader('HOANBS', 'fred',start=start, end=end).resample('QS').first()
cons = DataReader('PCECC96', 'fred', start=start, end=end).resample('QS').first()
inv = DataReader('GPDIC1', 'fred', start=start, end=end).resample('QS').first()
pop = DataReader('CNP16OV', 'fred', start=start, end=end)
pop = pop.resample('QS').mean() # Convert pop from monthly to quarterly observations
recessions = DataReader('USRECQ', 'fred', start=start, end=end)
recessions = recessions.resample('QS').last()['USRECQ'].iloc[1:]
# Get in per-capita terms
N = labor['HOANBS'] * 6e4 / pop['CNP16OV']
C = (cons['PCECC96'] * 1e6 / pop['CNP16OV']) / 4
I = (inv['GPDIC1'] * 1e6 / pop['CNP16OV']) / 4
Y = C + I
# Log, detrend
y = np.log(Y).diff()[1:]
c = np.log(C).diff()[1:]
n = np.log(N).diff()[1:]
i = np.log(I).diff()[1:]
rbc_data = pd.concat((y, n, c), axis=1)
rbc_data.columns = ['output', 'labor', 'consumption']
Fig. 3 shows the resulting time series.
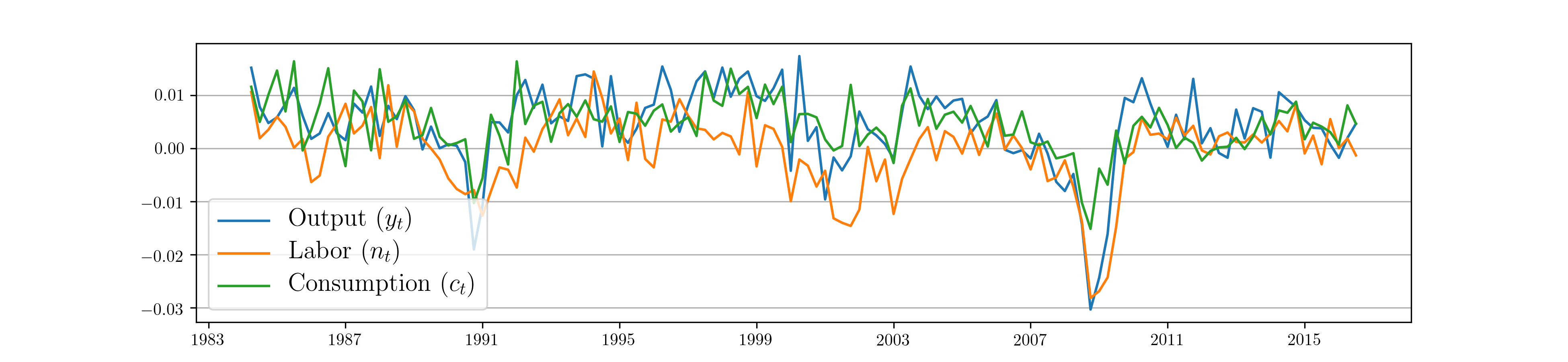
Fig. 3 US output, labor, and consumption time series 1984:Q1 - 2016:Q4.
| [4] | Note that this simple RBC model is presented for illustration purposes and so we aim for brevity and clarity of exposition rather than a state-of-the-art description of the economy. |
Parameter estimation¶
In order to accomodate parameter estimation, we need to introduce a couple of new ideas, since the generic state space model described above considers matrices with known values. In particular (following the notation in Chapter 7 of [10]), suppose that the unknown parameters are collected into a vector \(\psi\). Then each of the state space representation matrices can be considered as, and written as, a function of the parameters. For example, to take into account the dependence on the unknown parameters, we write the design matrix as \(Z_t(\psi)\).
The three methods for parameter estimation considered in this paper perform filtering, smoothing, and / or simulation smoothing iteratively, where each iteration has a (generally) different set of parameter values. Given this iterative approach, it is clear that in order to perform parameter estimation we will need two new elements: first, we must have the mappings from parameter values to fully specified system matrices; second, the iterations must begin with some initial parameter values and these must be specified.
The first element has already been introduced in the three examples above, since the state space matrices were written with known values (such as \(1\) and \(0\)) as well as with unknown parameters (for example \(\phi\) in the ARMA(1,1) model). The second element will be described separately for each of parameter estimation methods, below.